Ricerca

Panoramica

  • Studio le teorie quantistiche dei campi fortemente interagenti (QFT) — il quadro che unisce meccanica quantistica e relatività ristretta, e descrive le particelle come eccitazioni di campi sottostanti.
  • Il mio principale interesse riguarda le teorie conformi dei campi (CFT) — modelli altamente simmetrici che spesso governano la fisica alle grandi distanze o nei punti critici delle transizioni di fase.
  • Utilizzo la corrispondenza AdS2/CFT1 come un “ponte a doppio senso” tra QFT in uno spaziotempo curvo bidimensionale (AdS2) e CFT definite sul bordo unidimensionale di AdS2.
  • Il mio arsenale combina metodi moderni di bootstrap con tecniche classiche di QFT, come la teoria delle perturbazioni, la teoria dello scattering e il troncamento hamiltoniano.
  • Mi interesso anche ai difetti conformi, e ad approcci computazionali allo studio delle interazioni forti, come la teoria di gauge su reticolo e le reti tensoriali.

Ricerca dottorale

La mia ricerca riguarda la teoria quantistica dei campi (QFT) — il quadro che unisce meccanica quantistica e relatività ristretta. In questa prospettiva, le particelle sono “ondulazioni” o eccitazioni di campi sottostanti. La QFT è il linguaggio della fisica delle particelle, dove descrive le forze fondamentali della natura, ma compare anche in fisica della materia condensata, ad esempio nello studio della superconduttività o del magnetismo.

Un principio guida è il gruppo di rinormalizzazione (RG). Permette di seguire come una teoria cambia al variare della scala di energia — ingrandendo o riducendo lo “zoom”. Accade che teorie molto diverse ad alte energie (nell’ultravioletto, o UV) diventino simili a basse energie (nell’infrarosso, o IR). La teoria che emerge nell’IR è detta punto fisso IR. In molti casi fisicamente rilevanti, questi punti fissi sono teorie conformi dei campi (CFT) — QFT speciali invarianti a tutte le scale, o più precisamente invarianti sotto trasformazioni che preservano localmente gli angoli.

Schema dello spazio delle teorie, che mostra i flussi RG tra teorie UV e punti fissi IR, spesso CFT

Una delle sfide centrali della QFT è comprendere le teorie fortemente interagenti — situazioni in cui le interazioni sono così intense che non possono essere trattate come piccole correzioni a un modello semplice. Non è un’eccezione rara: la forza nucleare forte che lega protoni e neutroni a bassa energia è fortemente interagente, così come molti sistemi di materia condensata. Poiché le CFT rappresentano spesso punti speciali nello “spazio delle teorie” e sono più vincolate matematicamente delle QFT generiche, costituiscono punti di partenza naturali per esplorare il regime fortemente interagente. Oltre a questo interesse teorico, le CFT hanno numerose applicazioni: descrivono i punti critici delle transizioni di fase, la superficie d’universo in teoria delle stringhe e forniscono il fondamento del principio olografico, a cui passo ora.

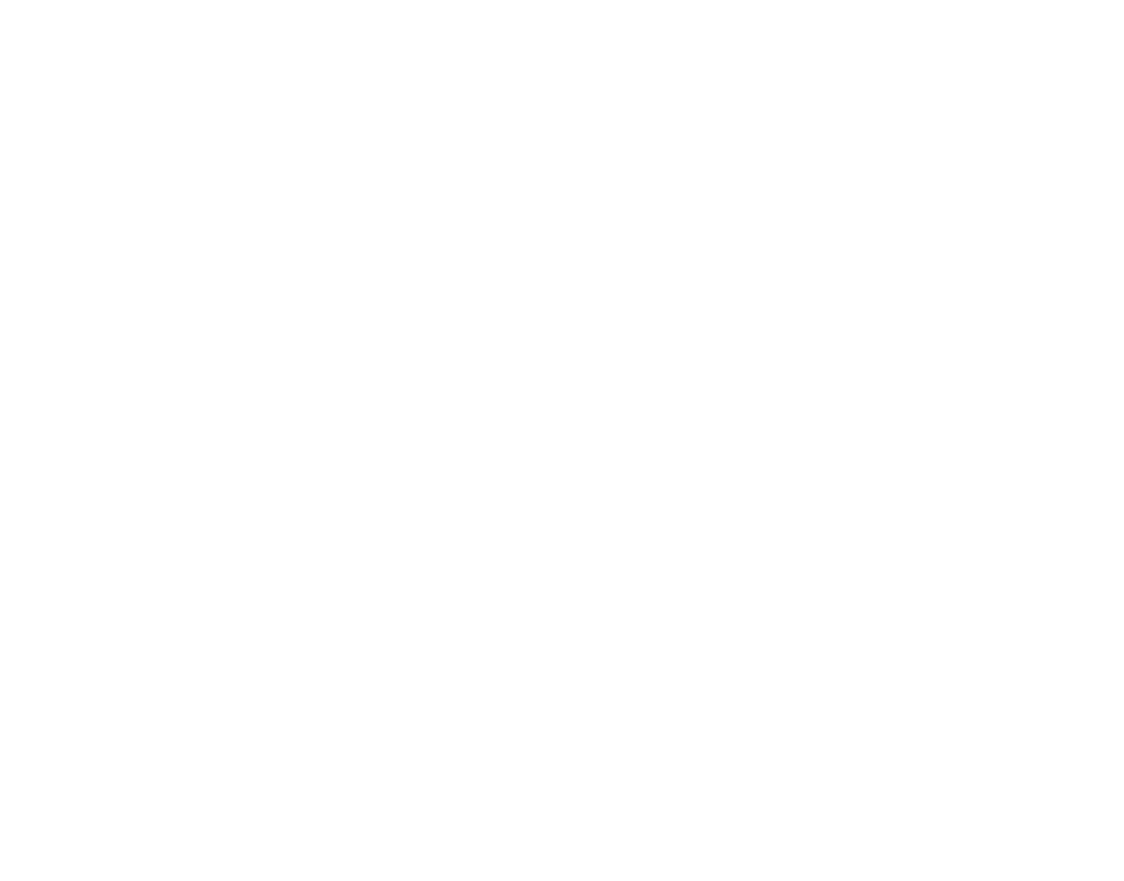
Un principio olografico: AdS2/CFT1

La formulazione più famosa — e probabilmente la più fruttuosa — del principio olografico è la corrispondenza AdS/CFT. Qui AdS indica lo spaziotempo anti–de Sitter, uno spaziotempo massimamente simmetrico a curvatura negativa. Può essere rappresentato come un “cilindro infinito”, il cui bordo corrisponde a spazio e tempo all’infinito, e la cui altezza rappresenta la direzione del tempo. Più fisicamente, è la geometria di un universo a curvatura negativa, privo di materia e radiazione, caratterizzato da una energia di vuoto negativa uniforme.

La corrispondenza afferma che certe CFT definite su questo bordo siano equivalenti a QFT con gravità dinamica nel bulk di AdS. In altre parole, la stessa fisica può essere descritta o da una QFT al bordo, o da una QFT con gravità attivata nel volume. Da qui il termine “olografico”: la fisica del bulk, in dimensione superiore, è interamente codificata nella teoria al bordo, in meno dimensioni — come un ologramma che immagazzina un’immagine 3D su una superficie 2D. In modo sorprendente, questa dualità collega due problemi tra i più difficili: la QFT fortemente interagente e la gravità quantistica.

Schema della corrispondenza AdS/CFT, che mostra lo spaziotempo AdS e una CFT definita sul suo bordo cilindrico

Sebbene l’olografia abbia stimolato progressi in molte dimensioni, i casi ad alta dimensionalità restano tecnicamente complessi: le CFT duali sono spesso poco comprese e i risultati non perturbativi scarsi. Al contrario, gli scenari a bassa dimensionalità — come le CFT 1D o 2D — sono più accessibili, sia numericamente (meno gradi di libertà), sia analiticamente, ad esempio con il bootstrap analitico, che sfrutta simmetrie e coerenza interna per vincolare lo spazio delle teorie possibili. Nella mia ricerca mi concentro sul caso non banale più semplice: la corrispondenza AdS2/CFT1. Qui la CFT duale è unidimensionale e particolarmente adatta alle nuove tecniche di bootstrap funzionale analitico sviluppate dal mio gruppo, oltre che a strumenti classici della QFT come il troncamento hamiltoniano.

Strumenti e obiettivi

La corrispondenza AdS/CFT offre due prospettive complementari:
- Sul lato bulk (dentro AdS2): utilizzo strumenti standard della QFT come la teoria delle perturbazioni, la teoria dello scattering (metodi di matrice-S) e il troncamento hamiltoniano (un’approssimazione numerica che riduce la teoria a un insieme finito di stati). Questi metodi sono adatti a studiare le dinamiche lontane dai punti fissi e a seguire l’evoluzione delle teorie sotto deformazioni.
- Sul lato del bordo (la CFT1): posso applicare anch’io strumenti di QFT, ma ho in più accesso al bootstrap conforme — un metodo moderno e non perturbativo che si basa unicamente su simmetria e autoconsistenza per restringere lo spazio dei punti fissi possibili.

Questi due punti di vista si completano. Il bootstrap vincola quali punti fissi conformi sono possibili, mentre i metodi di QFT mostrano come le teorie evolvono sotto deformazioni. Il mio obiettivo è usare entrambe le prospettive congiuntamente: capire come la dinamica fortemente interagente del bulk si codifichi nei dati della CFT al bordo e, reciprocamente, come la struttura della CFT illumini la dinamica della QFT.

In breve: rivisitare problemi classici della teoria quantistica dei campi con strumenti moderni, e interpretare le strutture matematiche che emergono dal bootstrap e dall’olografia in termini fisici.

Interessi paralleli

Difetti conformi

Mi interesso anche ai difetti conformi — tema del mio primo articolo. Un difetto è in generale un sottospazio a dimensionalità inferiore (linea, superficie o sottovarietà) che modifica una QFT. Ad esempio, in un reticolo di spin portato alla temperatura critica — descritto da una CFT — si può introdurre un difetto applicando un campo magnetico solo lungo una linea di spin. Il sistema risultante non è più invariante sotto l’intero gruppo conforme, ma se il difetto preserva la simmetria conforme su di sé (e la simmetria di rotazione intorno), si parla di teoria conforme con difetto (dCFT).

Dal punto di vista dell’RG, introdurre un difetto equivale a perturbare una teoria UV con un operatore localizzato, e seguire il flusso verso un nuovo punto fisso IR. I difetti diventano quindi sonde naturali dello spazio delle teorie: non solo arricchiscono il catalogo delle CFT, ma forniscono anche un modo controllato per esplorare nuove classi di universalità.

Fisicamente, le dCFT compaiono in molti contesti: dalle brane e loro intersezioni in teoria delle stringhe, alle linee e ai loop di Wilson in teoria di gauge, fino a impurità magnetiche e difetti cristallini in materia condensata. Forniscono dunque un quadro unificante che collega fenomeni provenienti da ambiti apparentemente molto diversi.

Teoria di gauge su reticolo e reti tensoriali

Prima di lavorare sulle CFT, ho avuto una breve esperienza con la teoria di gauge su reticolo — il quadro non perturbativo standard per lo studio della QCD a bassa energia, una QFT fortemente interagente. In questo approccio, lo spaziotempo è discretizzato in una griglia: i quark occupano i siti, i gluoni sono associati ai legami, e si usano algoritmi di Monte Carlo per campionare configurazioni e calcolare osservabili. Questo metodo è stato estremamente efficace, specialmente nella QCD su reticolo, ma il costo computazionale cresce rapidamente con la dimensione del sistema, rendendo molti problemi inaccessibili.

Un’alternativa promettente si basa sulle reti tensoriali, rappresentazioni compresse di stati quantistici molto grandi, già rivelatesi potenti in fisica della materia condensata. Invece di immagazzinare una quantità esponenziale di informazioni, le reti tensoriali catturano la struttura essenziale di uno stato in forma più compatta. In modo notevole, molti osservabili della teoria di gauge su reticolo possono essere riformulati in questo linguaggio, aprendo la strada all’uso di algoritmi efficienti sviluppati nella fisica dei molti corpi. È un settore di ricerca ancora molto attivo, con la speranza di rendere possibili domani calcoli che oggi sono inefficaci o addirittura fuori portata per la QCD su reticolo.